Neural Networks （神经网络）¶

Neural networks can be constructed using the torch.nn package.

神经网络可以使用 torch.nn 包构建。

Now that you had a glimpse of autograd, nn depends on autograd to define models and differentiate them. An nn.Module contains layers, and a method forward(input) that returns the output.

现在你已经对 autograd 有了一定的了解， nn 依赖于 autograd 来定义模型并区分它们。一个 nn.Module 包含多个层，以及一个返回 output 的方法 forward(input) 。

For example, look at this network that classifies digit images:

例如，看看这个用于对数字图像进行分类的网络：

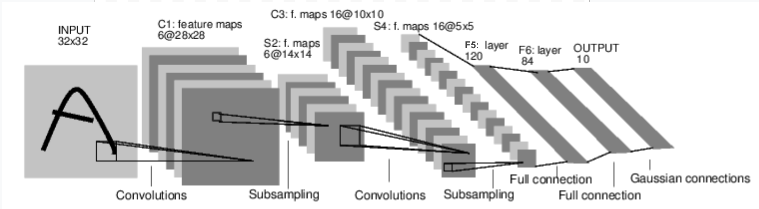
It is a simple feed-forward network. It takes the input, feeds it through several layers one after the other, and then finally gives the output.

这是一个简单的前馈网络。它接收输入，依次通过几层，最后给出输出。

A typical training procedure for a neural network is as follows:

一个神经网络的典型训练过程如下：

• Define the neural network that has some learnable parameters (or weights) 定义具有一些可学习参数（或权重）的神经网络
• Iterate over a dataset of inputs 遍历输入数据集
• Process input through the network 通过网络处理输入
• Compute the loss (how far is the output from being correct) 计算损失（输出与正确结果之间的误差）
• Propagate gradients back into the network's parameters 将梯度反向传播到网络的参数中
• Update the weights of the network, typically using a simple update rule: weight = weight - learning_rate * gradient 更新网络的权重，通常使用简单的更新规则： weight = weight - learning_rate * gradient

Define the network 定义网络¶

Let's define this network:

让我们定义这个网络：

You just have to define the forward function, and the backward function (where gradients are computed) is automatically defined for you using autograd. You can use any of the Tensor operations in the forward function.

您只需定义 forward 函数， backward 函数（计算梯度的函数）将自动使用 autograd 为您定义。您可以在 forward 函数中使用任何 Tensor 操作。

The learnable parameters of a model are returned by net.parameters()

模型的可学习参数由 net.parameters() 返回

Let's try a random 32x32 input. Note: expected input size of this net (LeNet) is 32x32. To use this net on the MNIST dataset, please resize the images from the dataset to 32x32.

让我们尝试一个随机的 32x32 输入。注意：该网络（LeNet）的预期输入大小为 32x32。要在 MNIST 数据集上使用此网络，请将数据集中的图像调整大小为 32x32。

Zero the gradient buffers of all parameters and backprops with random gradients:

将所有参数和反向传播的梯度缓冲区初始化为零，使用随机梯度：

注意：torch.nn 仅支持小批量。整个 torch.nn 包仅支持输入为小批量的样本，而不是单个样本。例如， nn.Conv2d 将接受一个 4 维张量 nSamples x nChannels x Height x Width 。如果你只有一个样本，只需使用 input.unsqueeze(0) 添加一个假的批量维度。

Before proceeding further, let's recap all the classes you've seen so far.

在进一步进行之前，让我们回顾一下你迄今为止所看到的全部课程。

Recap （总结）:

• torch.Tensor - A multi-dimensional array with support for autograd operations like backward(). Also holds the gradient w.r.t. the tensor.

  torch.Tensor - 支持自动求导操作（如 backward() ）的多维数组。同时存储张量的梯度。

• nn.Module - Neural network module. Convenient way of encapsulating parameters, with helpers for moving them to GPU, exporting, loading, etc.

  nn.Module - 神经网络模块。方便封装参数，并提供将参数移动到 GPU、导出、加载等辅助工具。

• nn.Parameter - A kind of Tensor, that is automatically registered as a parameter when assigned as an attribute to a Module.

  nn.Parameter - 一种 Tensor，当作为 Module 的属性赋值时，会自动注册为参数。

• autograd.Function - Implements forward and backward definitions of an autograd operation. Every Tensor operation creates at least a single Function node that connects to functions that created a Tensor and encodes its history.

  autograd.Function - 实现自动求导操作的向前和向后定义。每个 Tensor 操作至少创建一个 Function 节点，该节点连接到创建 Tensor 的函数并编码其历史。

At this point, we covered （此时，我们已涵盖：）:

• Defining a neural network

• 定义神经网络

• Processing inputs and calling backward

• 处理输入和调用反向

Still Left （还未涉及）:

• Computing the loss

  计算损失

• Updating the weights of the network

  更新网络的权重

Loss Function （损失函数）¶

A loss function takes the (output, target) pair of inputs, and computes a value that estimates how far away the output is from the target.

损失函数接收（输出，目标）这对输入，并计算一个值，该值估计输出与目标之间的误差。

There are several different loss functions under the nn package . A simple loss is: nn.MSELoss which computes the mean-squared error between the output and the target.

在 nn 包下有几种不同的损失函数。一个简单的损失函数是： nn.MSELoss ，它计算输出和目标之间的均方误差。

For example:

例如：

Now, if you follow loss in the backward direction, using its .grad_fn attribute, you will see a graph of computations that looks like this:

现在，如果您沿着 loss 的反方向进行跟踪，使用其 .grad_fn 属性，您将看到如下所示的计算图：

{.sourceCode
input -> conv2d -> relu -> maxpool2d -> conv2d -> relu -> maxpool2d
      -> flatten -> linear -> relu -> linear -> relu -> linear
      -> MSELoss
      -> loss

So, when we call loss.backward(), the whole graph is differentiated w.r.t. the neural net parameters, and all Tensors in the graph that have requires_grad=True will have their .grad Tensor accumulated with the gradient.

因此，当我们调用 loss.backward() 时，整个图相对于神经网络参数进行微分，图中所有具有 requires_grad=True 的张量的 .grad 属性将累积梯度。

For illustration, let us follow a few steps backward:

为了说明，让我们回顾几个步骤：

Backprop （反向传播）¶

To backpropagate the error all we have to do is to loss.backward(). You need to clear the existing gradients though, else gradients will be accumulated to existing gradients.

为了反向传播修正错误，我们只需运行 loss.backward() 。不过，您需要清除现有的梯度，否则梯度将累积到现有的梯度中。

Now we shall call loss.backward(), and have a look at conv1's bias gradients before and after the backward.

现在我们将调用 loss.backward() ，查看 conv1 的偏置梯度在反向传播前后的变化。

Now, we have seen how to use loss functions.

现在，我们已经看到了如何使用损失函数。

Read Later （稍后阅读）:

The neural network package contains various modules and loss functions that form the building blocks of deep neural networks. A full list with documentation is here.

神经网络模块包含各种模块和损失函数，这些构成了深度神经网络的基本构建块。完整列表及文档在此。

The only thing left to learn is （只剩下一件事需要学习）:

• Updating the weights of the network

更新网络权重

Update the weights （更新权重）¶

The simplest update rule used in practice is the Stochastic Gradient Descent (SGD):

最简单的实际应用中使用的更新规则是随机梯度下降（SGD）：

{.sourceCode
weight = weight - learning_rate * gradient

We can implement this using simple Python code:

我们可以使用简单的 Python 代码来实现这一点：

{.sourceCode
learning_rate = 0.01
for f in net.parameters():
    f.data.sub_(f.grad.data * learning_rate)

However, as you use neural networks, you want to use various different update rules such as SGD, Nesterov-SGD, Adam, RMSProp, etc. To enable this, we built a small package: torch.optim that implements all these methods. Using it is very simple:

然而，当您使用神经网络时，您希望使用各种不同的更新规则，如 SGD、Nesterov-SGD、Adam、RMSProp 等。为了实现这一点，我们构建了一个小型包： torch.optim ，它实现了所有这些方法。使用它非常简单：

{.sourceCode
import torch.optim as optim

# 创建你的优化器
optimizer = optim.SGD(net.parameters(), lr=0.01)

# 在你的训练循环中:
optimizer.zero_grad()   # 清零梯度缓冲区
output = net(input)
loss = criterion(output, target)
loss.backward()
optimizer.step()    # 进行更新

注意：观察梯度缓冲区必须使用 optimizer.zero_grad() 手动设置为零。这是因为梯度如反向传播部分所述是累积的。