英文原文:Deep Learning with PyTorch: A 60 Minute Blitz
作者: Soumith Chintala
原文地址:Deep Learning with PyTorch: A 60 Minute Blitz
中文译文:YukonKong/Chinese-version.Deep-Learning-with-PyTorch-A-60-Minute-Blitz
推荐下载此仓库中的 jupyter notebook 文件使用。
# 原文地址:https://pytorch.org/tutorials/beginner/blitz/autograd_tutorial.html
# 翻译转载:https://github.com/YukonKong/Chinese-version.Deep-Learning-with-PyTorch-A-60-Minute-Blitz
A Gentle Introduction to torch.autograd (关于 torch.autograd 的温和入门指南)¶
torch.autograd is PyTorch's automatic differentiation engine that
powers neural network training. In this section, you will get a
conceptual understanding of how autograd helps a neural network train.
torch.autograd 是 PyTorch 的自动微分引擎,为神经网络训练提供动力。在本节中,您将获得对 autograd 如何帮助神经网络训练的概念性理解。
Background (背景知识)¶
Neural networks (NNs) are a collection of nested functions that are executed on some input data. These functions are defined by parameters (consisting of weights and biases), which in PyTorch are stored in tensors.
神经网络(NNs)是一系列嵌套函数的集合,这些函数在输入数据上执行。这些函数由参数(包括权重和偏移)定义,在 PyTorch 中这些参数存储在张量中。
Training a NN happens in two steps:
训练神经网络分为两个步骤:
Forward Propagation (向前传播): In forward prop, the NN makes its best guess about the correct output. It runs the input data through each of its functions to make this guess.
在前向传播中,神经网络对其正确的输出做出最佳猜测。它将输入数据通过其每个函数运算后做出猜测。
Backward Propagation (反向传播): In backprop, the NN adjusts its parameters proportionate to the error in its guess. It does this by traversing backwards from the output, collecting the derivatives of the error with respect to the parameters of the functions (gradients), and optimizing the parameters using gradient descent. For a more detailed walkthrough of backprop, check out this video from 3Blue1Brown.
在反向传播中,神经网络根据其猜测中的误差调整其参数。它是通过从输出反向遍历,收集函数参数的误差导数(梯度),并使用梯度下降法优化参数来实现的。要详细了解反向传播,请观看 3Blue1Brown 的这段视频。
Usage in PyTorch (在 PyTorch 中的应用)¶
Let's take a look at a single training step. For this example, we load
a pretrained resnet18 model from torchvision. We create a random data
tensor to represent a single image with 3 channels, and height & width
of 64, and its corresponding label initialized to some random values.
Label in pretrained models has shape (1,1000).
让我们来看一个训练步骤。在这个例子中,我们从 torchvision 加载一个预训练的 resnet18 模型。我们创建一个随机的数据张量来表示一张具有 3 个通道、高度和宽度为 64 的单个图像,以及其对应的 label 初始化为一些随机值。预训练模型中的标签形状为(1,1000)。
This tutorial works only on the CPU and will not work on GPU devices (even if tensors are moved to CUDA).
注意:这个教程只能在 CPU 上运行,无法在 GPU 设备上工作(即使张量被移动到 CUDA)。
import torch
from torchvision.models import resnet18, ResNet18_Weights
model = resnet18(weights=ResNet18_Weights.DEFAULT)
data = torch.rand(1, 3, 64, 64)
labels = torch.rand(1, 1000)
Next, we run the input data through the model through each of its layers to make a prediction. This is the forward pass.
然后,我们将输入数据通过模型的每一层进行预测。这是正向传播。
prediction = model(data) # 正向传播
We use the model's prediction and the corresponding label to calculate
the error (loss). The next step is to backpropagate this error through
the network. Backward propagation is kicked off when we call
.backward() on the error tensor. Autograd then calculates and stores
the gradients for each model parameter in the parameter's .grad
attribute.
我们使用模型的预测结果和相应的真实标签来计算误差( 损失 )。下一步是将此误差反向传播到网络中。当我们调用 .backward() 在误差张量上时,开始反向传播。然后 Autograd 计算每个模型参数的梯度并存储到参数的 .grad 属性中。
loss = (prediction - labels).sum()
loss.backward() # 反向传播
Next, we load an optimizer, in this case SGD with a learning rate of 0.01 and momentum of 0.9. We register all the parameters of the model in the optimizer.
接下来,我们加载一个优化器,在本例中是学习率为 0.01、动量为 0.9 的 SGD,并将模型的所有参数注册到优化器中。
optim = torch.optim.SGD(model.parameters(), lr=1e-2, momentum=0.9)
Finally, we call .step() to initiate gradient descent. The optimizer
adjusts each parameter by its gradient stored in .grad.
最后,我们调用 .step() 来启动梯度下降。优化器使用存储在 .grad 中的梯度的值调整每个参数。
optim.step() # 梯度下降
At this point, you have everything you need to train your neural network. The below sections detail the workings of autograd - feel free to skip them.
此时,您已经拥有了训练神经网络所需的一切。下文各节详细介绍了 autograd 的工作原理——您可以自由地跳过它们。
Differentiation in Autograd (自动微分中的微分过程)¶
Let's take a look at how autograd collects gradients. We create two
tensors a and b with requires_grad=True. This signals to
autograd that every operation on them should be tracked.
让我们看看 autograd 如何收集梯度。我们添加参数 requires_grad=True 创建两个张量 a 和 b 。这向 autograd 发出信号,表明对它们的每个操作都应该被追踪。
import torch
a = torch.tensor([2., 3.], requires_grad=True)
b = torch.tensor([6., 4.], requires_grad=True)
We create another tensor Q from a and b.
我们从 a 和 b 创建另一个张量 Q 。
$$Q = 3a^3 - b^2$$
Q = 3*a**3 - b**2
Let's assume a and b to be parameters of an NN, and Q to be the
error. In NN training, we want gradients of the error w.r.t. parameters,
i.e.
让我们假设 a 和 b 是神经网络的参数, Q 是误差。在神经网络训练中,我们希望得到误差相对于参数的梯度,即:
$$\frac{\partial Q}{\partial a} = 9a^2$$
$$\frac{\partial Q}{\partial b} = -2b$$
When we call .backward() on Q, autograd calculates these gradients
and stores them in the respective tensors' .grad attribute.
当我们在 Q 上调用 .backward() 时,autograd 计算这些梯度并将它们存储在相应张量的 .grad 属性中。
We need to explicitly pass a gradient argument in Q.backward()
because it is a vector. gradient is a tensor of the same shape as Q,
and it represents the gradient of Q w.r.t. itself, i.e.
我们需要显式地传递一个 gradient 参数到 Q.backward() ,因为它是一个向量。 gradient 是与 Q 形状相同的张量,它代表了 Q 相对于自身的梯度,即
$$\frac{dQ}{dQ} = 1$$
Equivalently, we can also aggregate Q into a scalar and call backward
implicitly, like Q.sum().backward().
等效地,我们也可以将 Q 聚合为一个标量,并隐式地调用 Q.sum().backward() 。
external_grad = torch.tensor([1., 1.])
Q.backward(gradient=external_grad)
Gradients are now deposited in a.grad and b.grad
梯度现在存储在 a.grad 和 b.grad
# 检查收集的梯度是否正确
print(9*a**2 == a.grad)
print(-2*b == b.grad)
tensor([True, True]) tensor([True, True])
Optional Reading - Vector Calculus using autograd (可选阅读 - 使用 autograd 的向量微积分)¶
Mathematically, if you have a vector valued function $\vec{y}=f(\vec{x})$, then the gradient of $\vec{y}$ with respect to $\vec{x}$ is a Jacobian matrix $J$:
$$\begin{aligned} J = \left(\begin{array}{cc} \frac{\partial \bf{y}}{\partial x_{1}} & ... & \frac{\partial \bf{y}}{\partial x_{n}} \end{array}\right) = \left(\begin{array}{ccc} \frac{\partial y_{1}}{\partial x_{1}} & \cdots & \frac{\partial y_{1}}{\partial x_{n}}\\ \vdots & \ddots & \vdots\\ \frac{\partial y_{m}}{\partial x_{1}} & \cdots & \frac{\partial y_{m}}{\partial x_{n}} \end{array}\right) \end{aligned}$$
Generally speaking, torch.autograd is an engine for computing
vector-Jacobian product. That is, given any vector $\vec{v}$, compute
the product $J^{T}\cdot \vec{v}$
If $\vec{v}$ happens to be the gradient of a scalar function $l=g\left(\vec{y}\right)$:
$$\vec{v} = \left(\begin{array}{ccc}\frac{\partial l}{\partial y_{1}} & \cdots & \frac{\partial l}{\partial y_{m}}\end{array}\right)^{T}$$
then by the chain rule, the vector-Jacobian product would be the gradient of $l$ with respect to $\vec{x}$:
$$\begin{aligned} J^{T}\cdot \vec{v}=\left(\begin{array}{ccc} \frac{\partial y_{1}}{\partial x_{1}} & \cdots & \frac{\partial y_{m}}{\partial x_{1}}\\ \vdots & \ddots & \vdots\\ \frac{\partial y_{1}}{\partial x_{n}} & \cdots & \frac{\partial y_{m}}{\partial x_{n}} \end{array}\right)\left(\begin{array}{c} \frac{\partial l}{\partial y_{1}}\\ \vdots\\ \frac{\partial l}{\partial y_{m}} \end{array}\right)=\left(\begin{array}{c} \frac{\partial l}{\partial x_{1}}\\ \vdots\\ \frac{\partial l}{\partial x_{n}} \end{array}\right) \end{aligned}$$
This characteristic of vector-Jacobian product is what we use in the
above example; external_grad represents $\vec{v}$.
Computational Graph (计算图)¶
Conceptually, autograd keeps a record of data (tensors) & all executed operations (along with the resulting new tensors) in a directed acyclic graph (DAG) consisting of Function objects. In this DAG, leaves are the input tensors, roots are the output tensors. By tracing this graph from roots to leaves, you can automatically compute the gradients using the chain rule.
概念上,autograd 在一个由函数对象组成的有向无环图(DAG)中记录数据(张量)和所有执行的操作(以及产生的新张量)。在这个 DAG 中,叶子是输入张量,根是输出张量。通过从根到叶子的追踪这个图,你可以使用链式法则自动计算梯度。
In a forward pass, autograd does two things simultaneously:
在正向传播中,autograd 同时执行两件事:
- run the requested operation to compute a resulting tensor, and 执行所需的操作以计算结果张量,并
- maintain the operation's gradient function in the DAG. 保持 DAG 中梯度函数的运行。
The backward pass kicks off when .backward() is called on the DAG
root. autograd then:
当在 DAG 根节点上调用 .backward() 时,开始反向传播。 autograd 则会:
- computes the gradients from each
.grad_fn, 计算每个 .grad_fn 的梯度 - accumulates them in the respective tensor's
.gradattribute, and 将它们累积在相应张量的 .grad 属性中,并且 - using the chain rule, propagates all the way to the leaf tensors. 使用链式法则,传播至所有叶张量。
Below is a visual representation of the DAG in our example. In the
graph, the arrows are in the direction of the forward pass. The nodes
represent the backward functions of each operation in the forward pass.
The leaf nodes in blue represent our leaf tensors a and b.
以下是本例中 DAG 的视觉表示。在图中,箭头表示正向传播的方向。节点代表正向传播中每个操作的逆向函数。蓝色叶子节点代表我们的叶子张量 a 和 b 。
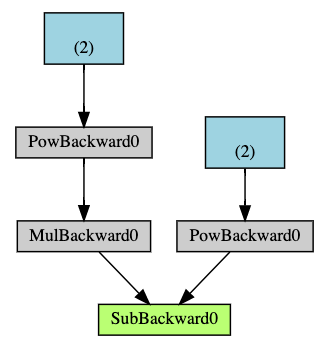
An important thing to note is that the graph is recreated from scratch; after each.backward() call, autograd starts populating a new graph. This isexactly what allows you to use control flow statements in your model;you can change the shape, size and operations at every iteration ifneeded.
注意:需要注意的一个重要事项是,该图是从头开始重建的;在每次 .backward() 调用后,autograd 开始填充一个新的图。这正是允许你在模型中使用控制流语句的原因;如果需要,你可以在每次迭代中更改形状、大小和操作。
Exclusion from the DAG (排除在 DAG 之外)¶
torch.autograd tracks operations on all tensors which have their
requires_grad flag set to True. For tensors that don't require
gradients, setting this attribute to False excludes it from the
gradient computation DAG.
torch.autograd 跟踪所有将 requires_grad 标志设置为 True 的张量上的操作。对于不需要梯度的张量,将此属性设置为 False 将使其排除在梯度计算有向无环图(DAG)之外。
The output tensor of an operation will require gradients even if only a
single input tensor has requires_grad=True.
操作输出的张量即使只有一个输入张量带有 requires_grad=True ,也需要梯度。
x = torch.rand(5, 5)
y = torch.rand(5, 5)
z = torch.rand((5, 5), requires_grad=True)
a = x + y
print(f"Does `a` require gradients?: {a.requires_grad}")
b = x + z
print(f"Does `b` require gradients?: {b.requires_grad}")
Does `a` require gradients?: False Does `b` require gradients?: True
In a NN, parameters that don't compute gradients are usually called frozen parameters. It is useful to "freeze" part of your model if you know in advance that you won't need the gradients of those parameters (this offers some performance benefits by reducing autograd computations).
在神经网络(NN)中,不计算梯度的参数通常被称为冻结参数。如果你事先知道不需要某些参数的梯度,冻结模型的一部分是有用的(这通过减少自动微分计算来提供一些性能优势)。
In finetuning, we freeze most of the model and typically only modify the classifier layers to make predictions on new labels. Let's walk through a small example to demonstrate this. As before, we load a pretrained resnet18 model, and freeze all the parameters.
在微调中,我们冻结模型的大部分参数,通常只修改分类层以对新标签进行预测。让我们通过一个小例子来演示这一点。和之前一样,我们加载一个预训练的 resnet18 模型,并冻结所有参数。
from torch import nn, optim
model = resnet18(weights=ResNet18_Weights.DEFAULT)
# 冻结这个网络中的所有参数
for param in model.parameters():
param.requires_grad = False
Let's say we want to finetune the model on a new dataset with 10
labels. In resnet, the classifier is the last linear layer model.fc.
We can simply replace it with a new linear layer (unfrozen by default)
that acts as our classifier.
假设我们想在包含 10 个标签的新数据集上微调模型。在 ResNet 中,分类器是最后一个线性层 model.fc 。我们可以简单地用一个新的线性层(默认未冻结)来替换它,作为我们的分类器。
model.fc = nn.Linear(512, 10)
Now all parameters in the model, except the parameters of model.fc,
are frozen. The only parameters that compute gradients are the weights
and bias of model.fc.
现在模型中所有参数,除了 model.fc 的参数外,都被冻结。唯一计算梯度的参数是 model.fc 的权重和偏置。
# 仅优化分类器
optimizer = optim.SGD(model.parameters(), lr=1e-2, momentum=0.9)
Notice although we register all the parameters in the optimizer, the only parameters that are computing gradients (and hence updated in gradient descent) are the weights and bias of the classifier.
尽管我们在优化器中注册了所有参数,但只有分类器的权重和偏置在计算梯度(因此更新在梯度下降中)。
The same exclusionary functionality is available as a context manager in torch.no_grad()
同样的排除性功能也可作为上下文管理器在 torch.no_grad() 中使用。





Comments NOTHING